If you have some experience in corporate finance and investment analysis, you already know different ways to calculate project’s Terminal Value (TV). In most cases, the default way is to calculate PV of future CFs with Gordon growth model.

Gordon growth model

The most used formula is quite easy:

Where:

• D0 = Cash flows at a future point in time which is immediately prior to N+1, or at the end of period N, which is the final year in the projection period
• k = Discount Rate
• g = Growth Rate

Most of the times when I see a DCF model, Terminal Value is calculated with the formula above. Wikipedia is quoting this formula as a go-to.

What’s actually wrong?

When using the formula above, you imply that D1 = D0*(1+g). And that is not always true. Well, for evaluation of a company or a project such assumption is actually false most of the time.

Let’s see an example of simple FCF calculation for a company in two last projection periods:

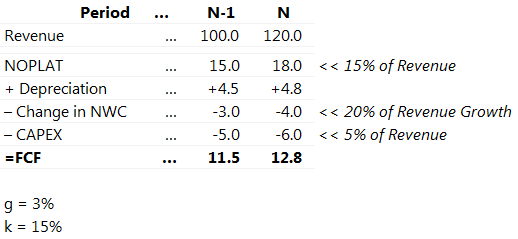
In order to calculate Terminal Value based on this most of people (just as Wikipedia tells you) will do the following math:

Terminal value = 12.8 x (1+3%)/(15%-3%) = 109.9

Seems legit?

Let’s take a closer look at what we actually did there with the CF. In the table below I explicitly calculated the implied Cash Flow for N+1 Period. As we implied, that D1 = D0*(1+g), I actually just multiplied by (1+3%) every component of the CF.

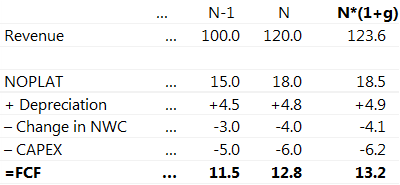
Try to spot what’s wrong:

• Change in NWC is actually greater than the change in Revenue. It is not even close to 25% NWC/Revenue ratio used in the projection period.
• There is a constant delta between CAPEX and Depreciation of 1.2 or 25% which is preserved through future perpetuity. Probably, NOPLAT would also need to be reconsidered as Depreciation is a part of it.

There are other ways to demonstrate same discrepancies in resulting values.

The reasons for getting such absurd numbers are that D0*(1+g) formula is actually a convenient shortcut to calculate “Dividend/CashFlow in the first terminal period”. Growth Rate in Gordon model formula should apply to CF/Dividends. Yet we determine g based on estimated economic growth, which corresponds to revenue growth. In the end, it turns out that we took parameters which do not scale linearly with the growth rate and then tried to implicitly scale them in Gordon Growth formula

From now on I will be focusing on NWC as it is easier to illustrate, requires less judgment on company’s performance and has a greater impact than CAPEX-Depreciation issue.

What are the implications?

If we recalculate Change in NWC of N+1 period using our 25% ratio, we can now calculate Terminal Value = D1 /(15%-3%). New figures are colored green. Red corresponds to the previous calculation of (1+3%) multiplication.

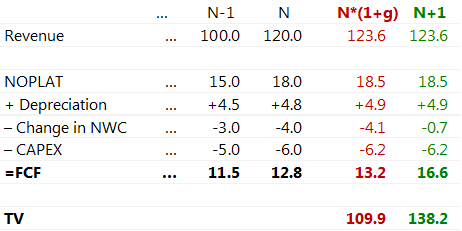
First, now Change in NWC makes much more sense.

Second, there is 25% difference between old and new Terminal Values. Depending on other inputs, this may result in 5% difference of Enterprise or Equity value of a company.

How to modify your Terminal value calculations?

There are multiple options:

1. Explicitly calculate the CashFlow for the N+1 period like we did in the example above

• Best option in my opinion. That way you may double-check your assumptions on every CashFlow component.

1. Ignore it. There are 2 considerations:

• The resulting error may be greater or smaller depending on internal business ratios and on N-1 period parameters. If your growth in N period is close to Terminal Growth Rate then the error will be negligible. But if your project has significant growth rate or one-off factors in N period, the error will be huge.
• Ignoring the error usually results in lesser TV, which may be regarded as a conservative approach.

1. Use calculation hacks to keep error under control. I have seen people using various ways to adjust the CF used for Gordon Formula. Although they do not remove calculation error, they guarantee, that its value is fairly small:

• Set Change in NWC to 0
• Set CAPEX = Depreciation

Final thoughts

Gordon Growth Model is great as it allows for a simple and rememberable way to simplify quite complex value calculations. The formula is one of the fundamentals of modern investment analysis. Yet it has its limitations and hidden assumptions that should be taken into consideration when creating your own financial models.