В этой статье описаны стратегии и алгоритмы поиска решения для игры Wordle, оценена их практическая эффективность, приведены оптимальные слова для начала игры. Как идеи для обсуждения будут озвучены размышления по связанной теме.

Об игре Wordle

Wordle(wikipedia) - браузерная игра, в которой загадывается слово из 5 букв, которое игрок должен отгадать за 6 попыток.

После каждой попытки отгадать загаданное слово буквы слова-попытки помечаются одним из трёх цветов:

• Зелёный - правильная буква на правильном месте в слове
• Жёлтый - буква есть в слове, но на другой позиции
• Серый - буква в слове отсутствует

Играть можно 1 раз в день (альтернативный вариант без ограничений). Загаданное слово в один день одинаково для всех игроков.

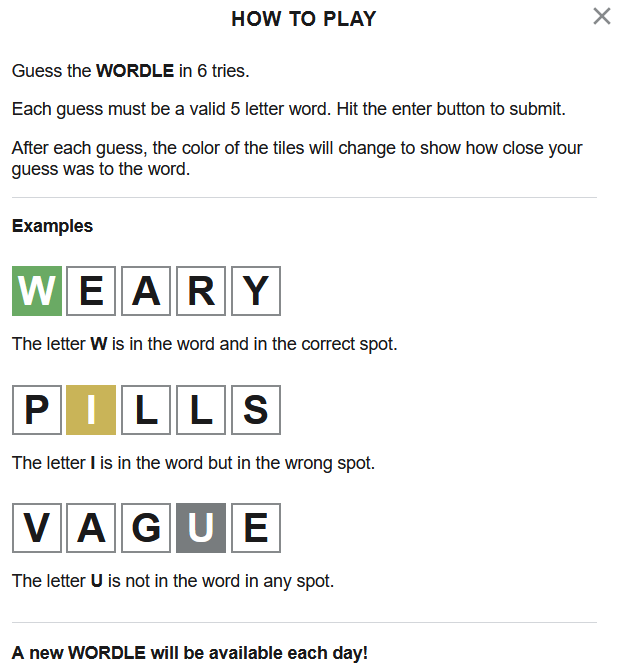
Кроме основных правил, есть неочевидные и скрытые особенности:

• Все слова, которые могут быть загаданы, находятся в открытом виде в коде игры. Список возможных слов загадок включает 2315 слов, изначально подобранных человеком.
• По исходному коду игры легко определить, какое слово загадано сегодня. Слова в упомянутом выше списке расположены в порядке дней, когда они будут загаданы. Зная слово, загаданное вчера, можно найти его в списке, следующее за ним слово будет сегодняшней загадкой.
• В качестве слова-попытки можно использовать только слова из заранее определённого списка из 13 тысяч слов. Список в открытом виде тоже находится в исходном коде игры. Если слово-попытка не входит в список, то игра его не примет.

Помимо основного режима игры, есть ещё сложный режим, в котором слова, вводимые для угадывания, обязательно должны использовать ранее полученные зелёные и жёлтые подсказки. Мы не будем пока его рассматривать.

Аудитория игры - несколько миллионов игроков. В 2022 году The New York Times купил игру за семизначную сумму в долларах.

1. Определим общие правила для стратегий и сформулируем логику за ними

Будем ориентироваться на правила Wordle, но брать более строгие предпосылки, чтобы избавиться от специфики конкретной реализации игры. Правила для стратегий:

• Знаем заранее, что загаданное слово входит в список из 13 тысяч слов
  • Это условие соответствует гипотезе, что мы стараемся угадать слово из конкретного языка, а не набор символов
• Не знаем заранее, что загаданное слово входит в список из 2315 возможных ответов
  • Формальные правила игры гарантируют игроку только то, что будет загадано корректное 5-буквенное слово. Все слова из списка 13 тысяч слов - корректные 5 буквенные слова.
  • Большинство алгоритмов и примеров, которые по поиску находятся в интернете, игнорируют это ограничение и рапортуют о 100% или близком к нему винрейте. Например: 99,4%, 99,7% и 100%.
  • Забегая вперёд, отмечу, что ограничение поиска 2315 словами даёт для почти всех стратегий 100% вероятность победы, так как количество возможных вариантов снижается на 80%
• Не используем данные о частоте использования слов в английском языке
  • Если мы рассматриваем Wordle как игру между людьми, то логично, что загаданное слово будет выбрано из более общеупотребимых слов. Такое слово проще придумать человеку, и это лучше для игры в перспективе, чтобы у отгадывающего не пропал интерес.
  • Использование данных о частоте распределения слов оправдано в том случае, если мы знаем, каким образом выбираются слова для загадывания. Но, в таком случае, это сильно похоже на то, как если бы мы сразу ограничились известными 2315 возможными ответами.
  • Некоторые стратегии, как, например, в этом очень интересном видео от 3Blue1Brown, используют данные о статистике распределения слов в английском языке для подбора слова-попытки и это существенно повышает успешность стратегии.

2. Целевые метрики

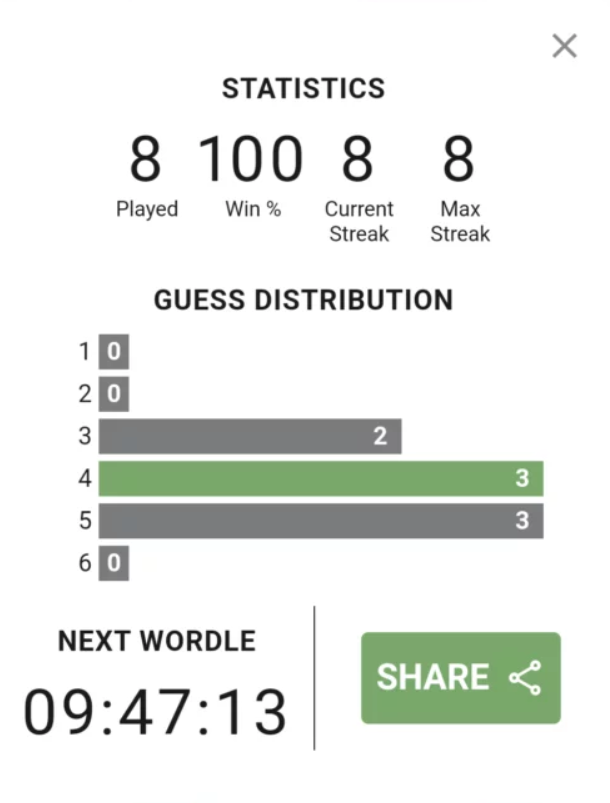
Игра предлагает игроку отслеживать две основных метрики:

1. Процент побед, когда слово было разгадано за 6 и менее ходов
2. Количество ходов, которое потребовалось для разгадывания слов в победных играх

В зависимости от целевой метрики выбранные стратегии будут отличны:

• Стратегия максимального процента побед должна стараться за первые 5 ходов собрать максимальную информацию о разгадываемом слове, максимально снизив множество оставшихся возможных ответов к 6 ходу
  • Идеальный сценарий реализации стратегии - когда перечень возможных вариантов ответов снижается до количества оставшихся ходов (например, один оставшийся возможным вариант к шестому ходу)
  • Если к шестому ходу не удалось сузить список возможных ответов до одного, то остаётся только полагаться на случайный выбор (ниже опишу более подробно, почему так)
• Стратегия минимизации количества ходов, наоборот, балансирует между сбором информации о разгадываемом слове и разгадыванием самого слова
  • Отличие от стратегии максимального процента побед в том, что если есть шанс угадать слово раньше шестого хода, то эту вероятность надо учитывать
  • За снижение количества необходимых ходов приходится расплачиваться более низким процентом побед при условии ограничения количества ходов.

Так как по определению нельзя выиграть, более чем в 100% случаев, то если у нас есть такие стратегии, то их можно оптимизировать по количеству ходов. Забегая вперёд, скажу, что большинство стратегий не обеспечивают 100% побед, и мы сможем продифференциаровать стратегии по эффективности.

На мой субъективный взгляд, мне приятнее иметь 100% винрейт со средним количеством ходов - 4, чем 90% винрейт со средним количеством ходов - 3.

Определились, что в качестве целевой метрики будем смотреть на процент побед.

2.1. Проблема выбора на 6-ом ходу

Интересно, что если к 6 ходу, после отбрасывания невозможных кандидатов, среди кандидатов в ответы осталось больше одного слова, то никакая эвристическая или вероятностная стратегия, кроме случайного выбора больше не работает.

Например к концу игры остались слова:

• stuff
• staff
• yrivd (да, это корректное слово)

Если у нас нет информации о том, как отбирались слова, то вероятность каждого из этих слов быть загаданным одинакова, и нет такой стратегии, которая могла бы дать процент победы больше, чем 1/3.

Самый популярный подход тестирования стратегий к Wordle, это тестировать их только на множестве 2315 слов-ответов. Даже когда авторы изначально “честно” ведут поиск ответов среди множества из 13 тысяч слов, то тестируются обычно на 2315 словах.

В таких сценариях может сложиться ситуация, что конкретная стратегия, даже при 2+ возможных ответах к 6 ходу, выбирает правильный ответ точнее, чем случайный выбор. На самом деле, это иллюзия, связанная с тем, что тестирование проводится на заранее определённом неизменном наборе данных. В терминологии ML это - случай избыточного переобучения модели (overfitting).

В теории, такими случаями можно было бы пренебречь. В ML при тестировании моделей часто используют случайную, но зафиксированную выборку (например, через фиксацию seed генератора случайных чисел), но:

• В машинном обучении модель потом проверяется на независимой выборке данных. Авторы стратегий для Wordle обычно больше ни на чем не проверяют.
• Хорошие алгоритмы для Wordle дают точность 95%+ или 99%+, соревнование идёт за десятые доли процентов угадывания крайних случаев. 0,1 процентного пункта - это эквивалент двух слов. В такой ситуации каждый случай некорректного угадывания становится значимым.

В итоге:

• Будем оценивать стратегии как на 2315 словах-ответах, так и на всем массиве из 13 тысяч слов
• Для упрощения расчётов, если к 6 ходу остаётся N вариантов ответов, то будем принимать вероятность выигрыша равной 1/N

Строго говоря, в некоторых простых стратегиях случайный выбор приходится делать раньше. Например, если после анализа 13 тысяч комбинаций, мы получаем одинаковые веса для разных слов. Чем проще стратегия, тем больше вероятность такой ситуации. Так как в большинстве случаев вероятность и влияние таких случаев ограничены, то для простоты расчётов в целом ими умышленно пренебрежём. Стратегии, где это будет более важно, я упомяну это отдельно.

3. Минимальный набор алгоритмов

Минимальный набор алгоритмов, без которого не обходится ни одна стратегия, включает в себя набор фильтров на основе озвученных правил игры:

1. Если буква была подсвечена зелёным, то она должна быть в загаданном слове на этой позиции
2. Если буква подсвечена жёлтым, то буква должна быть в загаданном слове и не может быть на этой позиции
3. Если буква подсвечена серым, то буквы не должно быть в загаданном слове

После применения фильтра следующее слово выбирается случайным образом из оставшихся возможными вариантов ответа.

Мне очень нравится, как была оценена и показана эффективность в видео от Games Computers Play. В видео тестирование проводилось на 2315 ответах, но с честной попыткой найти ответ среди 13 тыс. вариантов. На изображении ниже показана вероятность найти ответ за 6 ходов в зависимости от набора используемых фильтров:

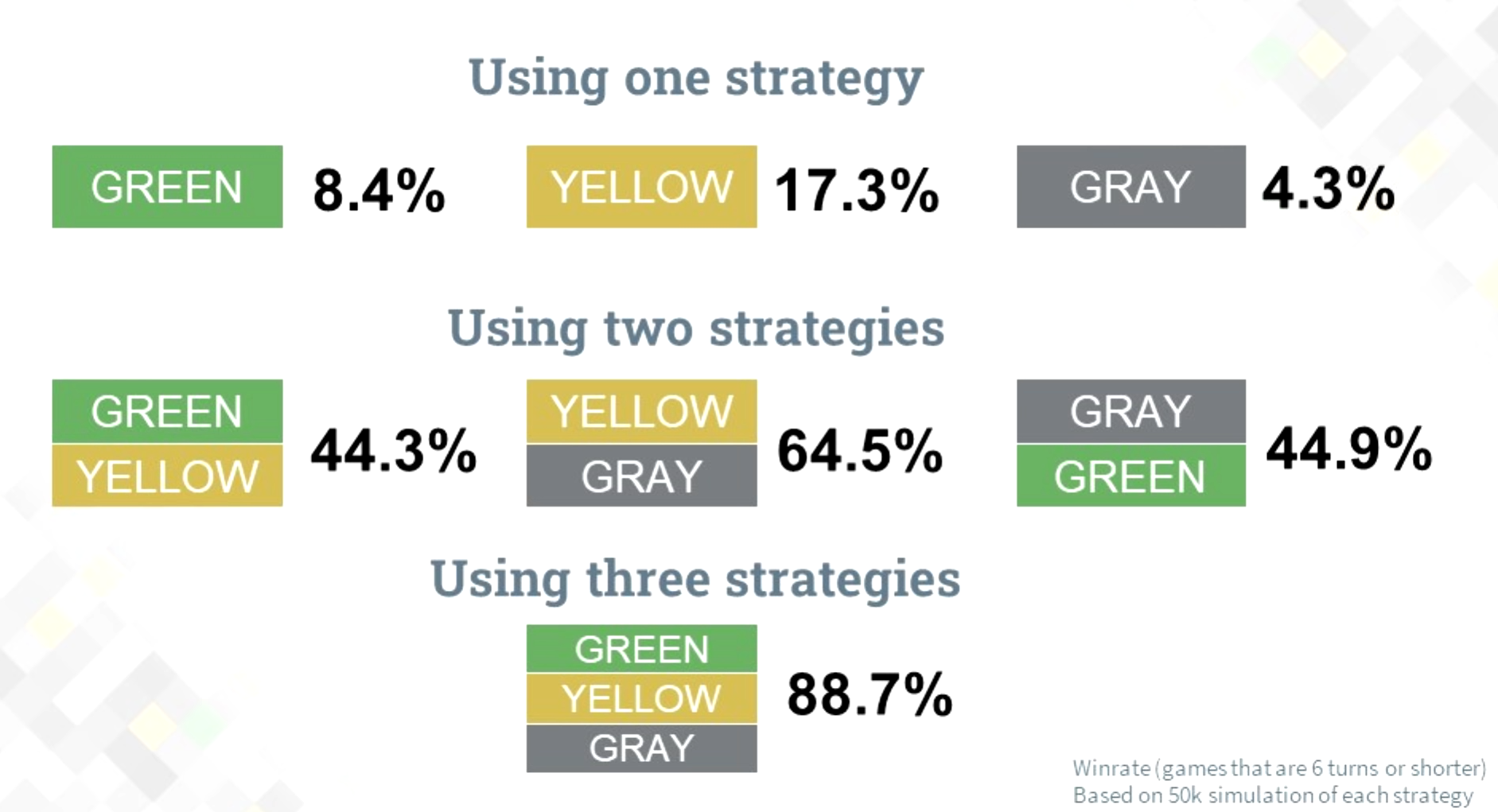
Совместное применение фильтров даёт мультипликативный рост эффективности. Но этих фильтров недостаточно для 100% победы. Поэтому, дальше, обычно, добавляются какие-то эвристики, которые мы будем смотреть в последщующем.

Процент побед за 6 ходов только за счёт фильтров на основе правил игры:

• на выборке 2315 ответов: 88,7%
• на выборке 13 тыс. ответов: 82,8%

Одна и та же непредвзятая стратегия на выборке из 2315 слов существенно эффективнее, чем на общем массиве слов. Оценивая стратегию только на 2315 отобранных слов, мы неявно подгоняем стратегию под более узкую выборку. В терминах ML - это “протечка данных” (data leakage).

4. Стратегии, основанные на частоте встречаемости букв

Логика стратегии: чем чаще в словах встречается та или иная ещё неизведанная буква -> больше вероятность получить зелёную или жёлтую буквы -> больше шанс угадать слово.

Примеры: видео, два, три и т.д.

Самый распространённый вариант стратегии:

1. Смотрим по каким буквам у нас ещё нет информации (ни серых, ни жёлтых, ни зелёных)
2. Оцениваем вероятность встретить эти буквы в оставшихся возможных ответах
3. Выбираем такого слово-попытку, состоящее из неопробованных букв с наибольшей вероятностью их встретить

Возможности для оптимизации стратегии:

• Выбирать следующее слово-попытку не из оставшихся вариантов ответов, а из всего доступного перечня слов, которые мы можем использовать (это даёт лишние 3% побед)
  • Например, наступил 5-й ход и у нас остаётся 4 потенциальных слова для ответа, которые отличаются только 1 буквой: sight, fight, might, night. Если перебирать последовательно по одному слова из этих 4 слов, то вероятность выиграть за 2 оставшихся хода - 50%. В таком случае, выгоднее попробовать такое слово как sniff, которое не является ответом, но в котором есть 3 буквы из 4. Результат такой попытки даст нам 100% вероятность определить итоговое слово за один ход и на следующем ходу выиграть партию. (В сложном режиме Wordle такая стратегия не сработает из-за обязательных требований использовать ранее полученные подсказки.)
• Оценивать не просто частоту использования букв, а вероятность встретить слово хотя бы с одной такой буквой (то есть, буква “a” в слове “arena” считается не как два вхождения, а как одно)
• Так как в начале игры мы всегда находимся в одних и тех же условиях, то мы можем заранее рассчитать определить лучшее слово на основе нашей стратегии. Формально уже на первом ходу есть три слова с максимальным рейтингом. Эту же оптимизацию будет применять в дальнейшем.

Процент побед за 6 ходов:

• на выборке 2315 ответов: 95,8%
• на выборке 13 тыс. ответов: 93,8%

Не знаю почему, но в этом видео автор достигает 96,6% процента побед на выборке 2315 слов. Спишем разницу на мои навыки программирования.

По итогам многократного моделирования лучшие слова для стратегий, основанных на частоте встречаемости букв: arose, aeros, soare.

Бонус: а что, если бы можно было использовать в качестве попытки любые 5 символов?

Такая стратегия не соответствует правилам Wordle, но было интересно попробовать, насколько требование вводить в качестве слова-попытки только корректные слова снижает вероятность победы.

Дополнительно два улучшения стратегии, после того, как определим 5 букв для попытки, будем располагать каждую букву на той позиции, где вероятность получить зелёную букву самая большая.

Процент побед за 6 ходов:

• на выборке 2315 ответов: 99,98%
• на выборке 13 тыс. ответов: 99,8%

В случае из 2315 слов стабильно не отгадывается одно и то же слово “tight”. В зависимости от случая, иногда алгоритм не может отгадать ещё одно или два слова.

Лучше комбинация букв для старта: raoes

5. Стратегии, основанные на шансах получить зелёные и жёлтые буквы

Гипотеза: когда удаётся отгадать зелёную букву, мы максимально приближаемся к разгадке загаданного слова. Чем больше шанс найти зелёную букву, тем лучше. После зелёных букв приоритет переходит на жёлтые буквы.

Стратегия:

1. Для каждого из слов-попыток перебираем оставшиеся варианты ответов и оцениваем все получившиеся комбинации зелёных, жёлтых, серых букв
2. Зададим вес для каждой из найденных букв. Например: 4 балла для новой зелёной буквы, 2 балл для новой жёлтой буквы, 1 баллов для новой серой буквы
3. Выбираем слово с наибольшим весом

Один из примеров реализации такого алгоритма в статье по ссылке.

Из очевидных минусов, высокая вычислительная сложность, так как нужно перебрать все возможные ответы для всех возможных слов-попыток. В случае попытки оценить алгоритм на всей выборке добавляется ещё многообразие уже найденных зелёных и жёлтых букв, с которыми надо сравнивать результаты попыток.

Процент побед за 6 ходов:

• на выборке 2315 ответов: 92,3%
• на выборке 13 тыс. ответов: не пробовал из-за невысокой эффективности на меньшей выборке и очень долгих расчётов

Лучше слово для старта: tares

6. Стратегии, основанные шансах максимально уменьшить оставшееся количество ответов

Гипотеза: чем больше шанс сузить итоговое пространство возможных ответов, тем лучше.

Стратегия:

1. Для каждого из слов-попыток перебираем оставшиеся варианты ответов и оцениваем сколько слов удалось исключить из списка возможных ответов
2. Выбираем слово с наибольшим количеством исключаемых ответов

Так как алгоритм ещё более вычислительно сложный, то я сориентировался на статью по ссылке, где автор тоже столкнулся с большой сложностью расчетов и реализовал алгоритм на языке C с исползованием многопоточности.

По словам автора алгоритм обеспечивает 100% решений при тестировании на 2315 словах. Проверил код на github, поиск ведётся честно по 13 тыс. словам.

Лучше слово для старта: roate

7. Стратегии, ориентированные на извлечение максимальной информации

Изначально я наткнулся на эту стратегию в этом репозитории на github. Совсем недавно вышло видео от 3Blue1Brown, в котором более подробно объясняется принцип стратегии.

Гипотеза: мы хотим выбрать такое слово, которое даст максимальное извлечение информации (энтропии). Идеальным словом-попыткой по этой стратегии, было бы такое слово, которое:

1. Даст наибольшее количество различных исходов в плане обновления зелёных, жёлтых и серых букв
2. Каждый из этих исходов даст одинаковое максимальное снижение множества оставшихся вариантов ответа. В нашем случае это эквивалентно тому, что вероятность всех исходов была бы одинакова.

Выше я очень упростил описание. Для всего этого есть более научные формулы, за деталями, рекомендую посмотреть упомянутое видео.

Процент побед за 6 ходов:

• на выборке 2315 ответов: 99,98% - стабильно не отгадывается только одно слово “berry”
• на выборке 13 тыс. ответов: 99,98

Лучше слово для старта: tares

8. Стратегия “tubes, fling, champ, wordy”

Стратегия из видео, в котором автор предлагает всегда начинать игру с конкретных 4 слов: “tubes, fling, champ, wordy”.

В стратегии есть тонкости, что в какой-то момент надо самостоятельно принимать решение по дальнейшему слову. Для простоты оценки я протестировал стратегию из этих четырёх слов и далее выбор слова на основе стратегии извлечения максимальной информации (пункт 6).

Процент побед за 6 ходов:

• на выборке 2315 ответов: 99,8%
• на выборке 13 тыс. ответов: 99,8%

Удивительно, но результаты оказываются не такими плохими. В зависимости от выбора стратегии на последние 2 хода, итоговая вероятность победы меняется. Она стабильно немного ниже, чем у соответсвующих чистых стратегий. Но возможность использовать 4 готовых слова, очень упрощает применение стратегии.

9. Бонус: Карта ответов для Wordle

Зачем писать алгоритм если можно просто дать дерево ответов? В своём видео и в репозитории на github автор составил конкретное дерево последовательностей слов-попыток в зависимости от найденных зелёных и жёлтых букв.

Очевидно, что для 2315 это “алгоритм” даёт 100% вероятность выигрыша и очень низкую вероятность для остальных возможных загаданных слов.

Сводные результаты

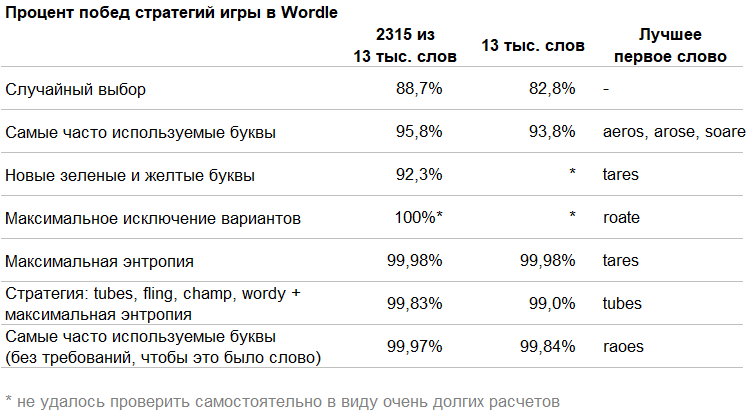
Выводы

Wordle очень простая и прозрачная игра. При разработке стратегии надо быть максимально осторожным в понимании её эффективности отдельно для конкретной игры, и для подобных игр в целом. Очень легко под видом сильной стратегии получить протечку данных, переобучение алгоритма или просто использование информации о конкретном списке загаданных слов.

Где та грань между жульничеством и честной стратегией? Что вы думаете?