Пример реальной задачи из своего опыта

Нужно проанализировать значения индекса NDVI для для конкретной географической точки. NDVI (Normalized Difference Vegetation Index - это индекс, который рассчитывается по данным спутниковой съёмки, и отражает здоровье растений, которые попали на снимок.

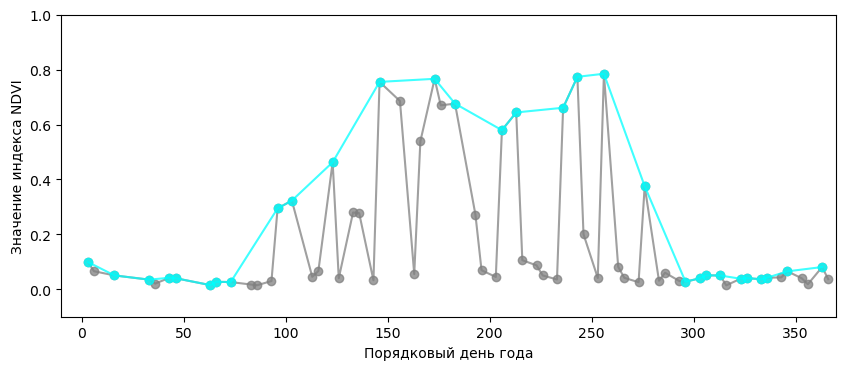
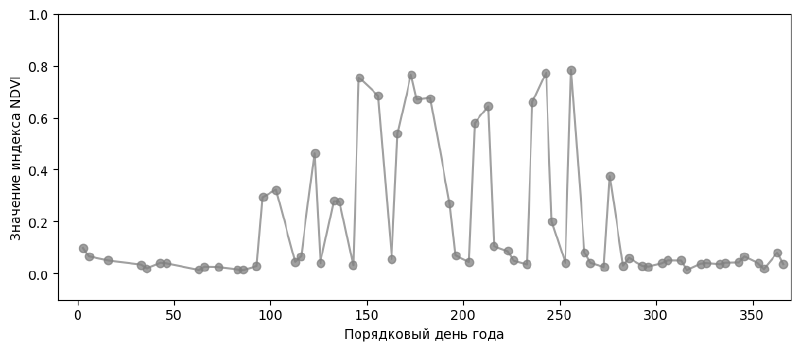
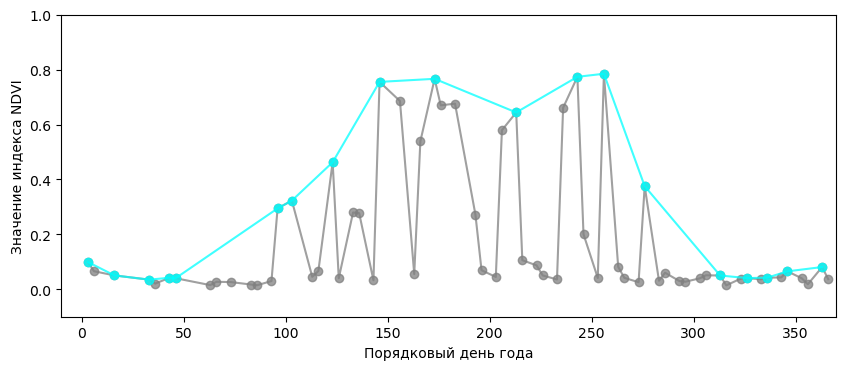
Скачиваем готовые или рассчитываем сами значения индекса NDVI с космического спутника за год. Если визуализировать полученные значения, то получится такой график:

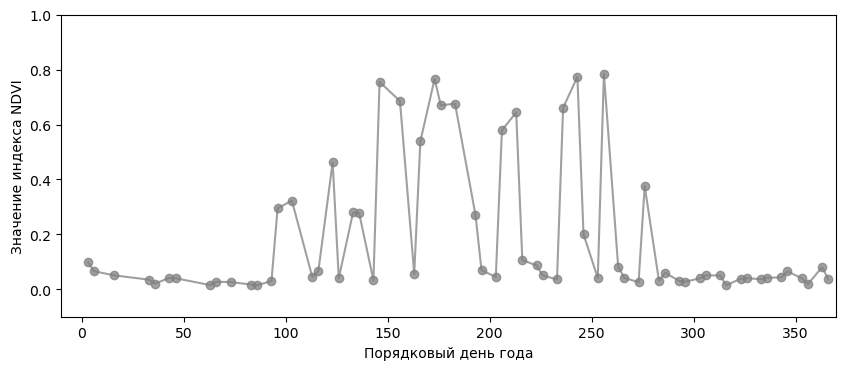
Из графика видно, что в период с 100 по 280 день значения индекса скачут от нуля до 0,8. Зная то, как индекс NDVI ведёт себя фундаментально, можно уверенно пометить значения ниже основного тренда как ошибочные. Например, на фотографии со спутника в этом месте было облако.

Задача: сгладить значения индексов и получить примерно такой тренд:

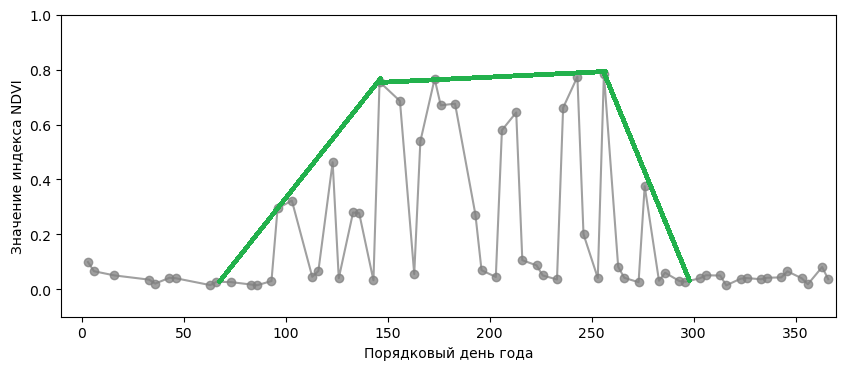
Другие примеры задач:

• Посчитать максимальные значения значение покупательного траффика, чтобы спрогнозировать запасы товара для торговой точки
• Гибкий расчёт границ ценовых каналов для биржевых торгов

Теоретическое описание алгоритма

Прокатываем виртуальный шар по точкам временного ряда, оставляя только те значения, которых коснётся шар.

Пример визуализации:

Алгоритм является подмножеством алгоритмов сглаживания по максимальным точкам.

Главная сильная сторона такого алгоритма то, что можно гибко настраивать параметры сглаживания временного ряда: длину окна в днях и рамки отклонения целевой метрики.

Как это работает

Последовательно проходимся по значениям временного ряда:

• Находясь в текущей точке-значении, выбираем 1 следующую точку, которой бы коснулся наш виртуальный шар. На примере ниже: мы находимся в точке “А”, следующей точкой будет точка “C”.
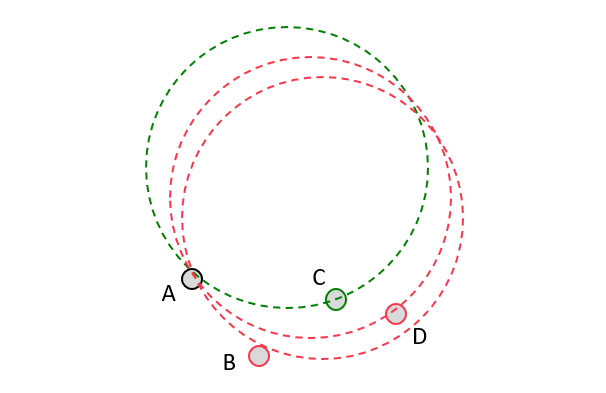
  • Иногда случается, что нет возможности выбрать следующую точку: нет точек в выбранном диапазоне или слишком большие отклонения метрики. В таком случае нужно выбирать свою стратегию под свои задачи: брать первую следующую точку, либо брать максимальную точку, либо брать точку, у которой вектор изменения минимален или другой вариант.
• Удаляем из временного ряда все точки, между нашей текущей точкой и следующей выбранной. В примере выше - удаляем точку “B”.
• Переходим в следующую точку. В примере выше - переходим в точку “С”.
• Повторяем алгоритм выбора

Выбор следующей точки

Самая сложная часть проектирования алгоритма - выбор следующей точки, которой коснётся шар.

Вариант решения наивным способом через геометрические формулы:

• Отобрать ближайшие следующие точки в пределах двух радиусов шара в днях
• Для каждой из отобранных точек рассчитать угол между горизонтальной осью и линией от текущей точки до центра виртуального шара
• Следующая точка, которой коснётся шар, будет иметь наибольшее значение этого угла

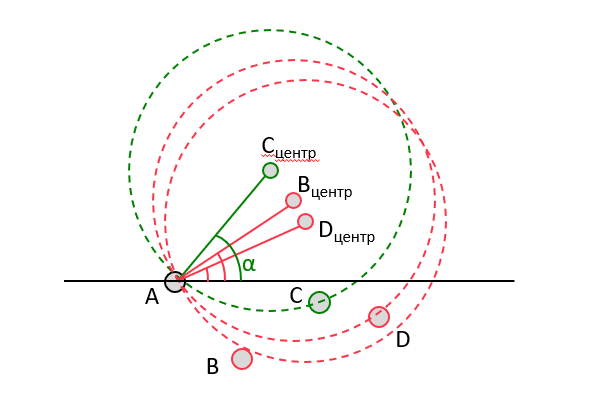
Это угол считается сложением двух углов:

• угол α1 между вектором от текущего значения к следующему и осью Х
• угол α2 между вектором от текущего значения к следующему и радиусом шара к текущей точке

Оба угла рассчитываются на базе формул из школьного курса геометрии:

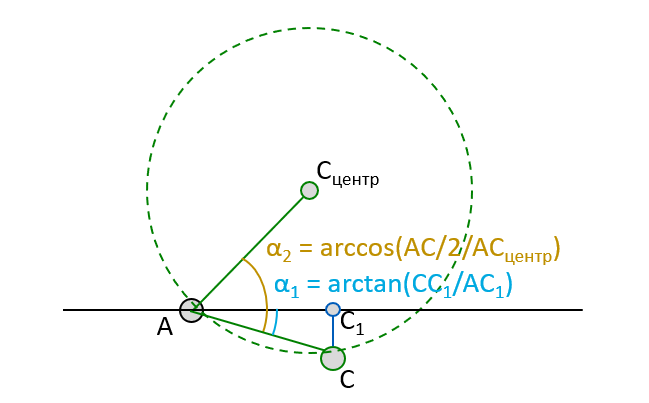
Пример реализации

Ниже представлен листинг кода на Python который реализует алгоритм расчёта угла на основе:

• значения и даты текущей точки
• значения и даты следующей точки
• радиуса шара в днях и в значениях метрики
• направления огибания - по верхней или по нижней границе временного ряда

На выходе функция выдаст положительное значение угла в радианах. Для выбора следующей точки во временном ряде нужно выбрать ту точку, которая имеет наибольший положительный угол.

import math

# Основная функция для расчёта угла
def calculate_angle_to_circle_center_from_measurement(curr_metric_value, curr_date, next_metric_value, next_date, radius_days, radius_metric, on_top=True):
    days_to_metric_coversion_ratio = radius_metric/radius_days
    
    x1 = 0
    y1 = 0
    
    x2 = (next_date - curr_date).days * days_to_metric_coversion_ratio
    y2 = float(next_metric_value - curr_metric_value)
    
    radius_metric_value = radius_days * days_to_metric_coversion_ratio
    try:
        return calculate_angle_to_circle_center(x1,y1,x2,y2,radius=radius_metric_value, on_top=on_top)
    except ValueError:
        # Заглушка на случай, если "шар" не касается следующей точки
        return -1000

    
def calculate_angle_to_circle_center(x1, y1, x2, y2, radius, on_top):
    chord_to_x_angle = math.atan((y2-y1)/(x2-x1))
   
    chord_length = calculate_chord_length(x1,y1,x2,y2)
    chord_lenth = math.sqrt((x2-x1)**2 + (y2-y1)**2)
    chord_to_circle_center_angle = math.acos(chord_lenth/2/radius)
    if on_top:
        angle_to_circle_center = chord_to_x_angle + chord_to_circle_center_angle
    else:
        angle_to_circle_center = -(chord_to_x_angle - chord_to_circle_center_angle)
    return angle_to_circle_center

def calculate_chord_length(x1, y1, x2, y2):
    x_delta = x2 - x1
    y_delta = y2 - y1
    chord_lenth = math.sqrt(x_delta**2 + y_delta**2)
    return chord_lenth

Примеры работы алгоритма

Возьмём за базу те значения NDVI, которые мы исследовали в начале статьи и визуализируем результаты сглаживания алгоритмом:

• сглаживание с радиусом шара - 60 дней и 0,3 значения индекса
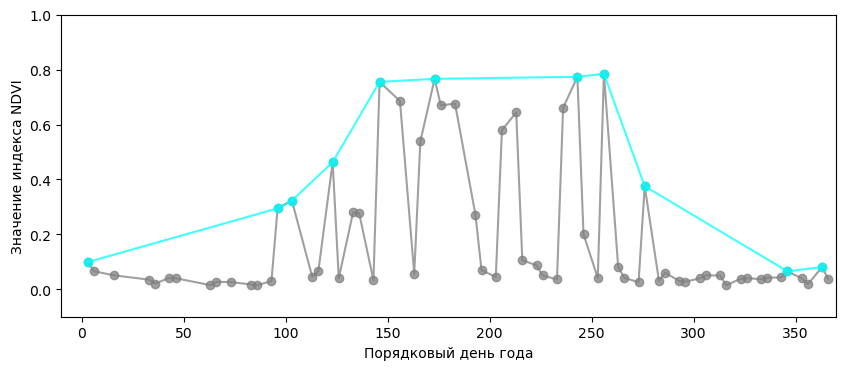
• сглаживание с радиусом шара - 45 дней и 0,5 значения индекса
• сглаживание с радиусом шара - 30 дней и 0,3 значения индекса