Допустим, нужно исследовать новую предметную область. В наличии ограниченное количество данных, например, выборка из 15 измерений (samples) с 10 предикторами в каждом. Вы хотите протестировать какие-то гипотезы, поискать возможные корреляции и в качестве логического вывода сделать минимальную регрессионную модель.
Сложные модели не подходят, когда данных мало
Сложные или комплексные модели - это модели, в которых много параметров и которые, как следствие, которые отражать большое количество закономерностей в обучающей выборке. Например, многослойные нейронные сети, деревья решений без ограничений по ветвлению и прочее.
Можно сформулировать такую гипотезу:
Если увеличивать сложность или комплексность модели, модель рано или поздно переобучится под обучающую выборку
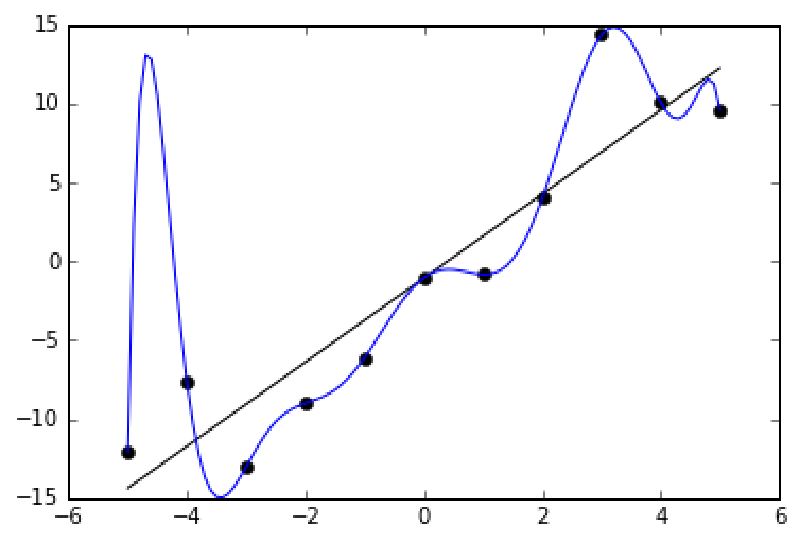
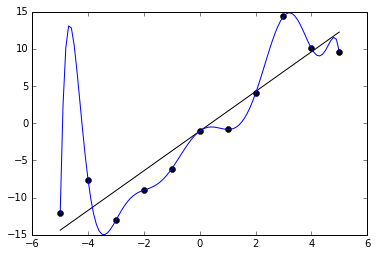
Переобучение (overfitting) - это частая проблема в машинном обучении, когда модель хорошо работает на обучающей выборки, но плохо работает на новых данных.
Выглядит переобучение примерно вот так (картинка с Wikipedia):
Стандартный способ бороться с переобучением - делить данные на обучающую и тестовую выборку. Учить модель на обучающей, проверять - на тестовой.
Но в нашем примере доступно только 15 замеров.
Во-первых, “разбрасываться” замерами и выделять 4 замера из 15 - слишком расточительно.
Во-вторых, даже если выделить 3-4 замера в тестовую выборку, то результаты валидации модели будут сильно зависеть от выбора каждого из тестовых измерений. Если выбрать другие 3-4 замера, то результаты получатся другими.
В условиях дефицита данных подходят только простые модели
Некоторые виды моделей сами по себе ограничены в возможной сложности:
- Линейная регрессия
- Опорные вектора
С этими моделями нужно только следить за балансом предикторов и размера выборки, но об этом ниже.
Другие модели можно искусственно ограничить в сложности:
- Нейронные сети - ограничить количество слоев и количество нейронов
- Деревья решений - ограничить глубину деревьев или количество листьев
Но с этими моделями нет универсального рецепта, как мало должно быть, например, нейронов, чтобы модель не переобучилась. Для этого используют тестовую выборку, которую мы не можем использовать по причинам выше.
Нужно следить за балансом предикторов и размера выборки
Переобучить можно даже линейную регрессию, если подать на вход модели избыточное количество предикторов.
Например, если количество предикторов сопоставимо с размером выборки, то это однозначно хорошая ситуация для переобучения. В нашем примере 10 предикторов на выборку из 15 измерений - это много.
Рекомендации как снижать количество предикторов:
- Оставлять только независимые предикторы (которые не коррелируют между собой)
- Оставлять только те предикторы, которые имеют хотя бы среднюю корреляцию с параметром, который мы пытаемся прогнозировать
Эти рекомендации также работают, когда в наличии есть много данных.
Выводы
- Если мало данных, то нельзя использовать сложные модели. Они с большой вероятностью переобучатся, а проверить наличие переобучение будет нельзя
- Лучше использовать простые модели, в фундамент которых уже заложены ограничения на сложность. Например, ту же линейную регрессию.
- Даже с простыми моделями нужно следить за балансом предикторов и размера выборки